Les templiers et le nombre d'Or

Les Templiers et le nombre d’Or

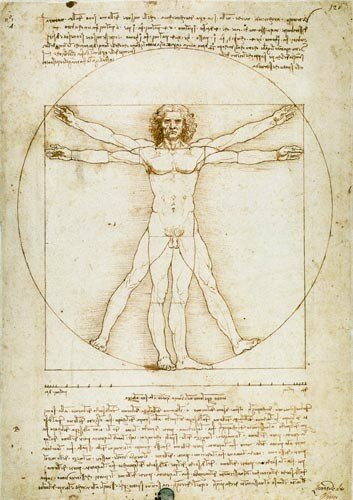
L'homme de vitruve - Leonard de vinci

Le lecteur sera peut-être surpris d’apprendre que les constructeurs de cathédrales du Moyen-âge, n’ont pas utilisé notre système métrique classique pour élaborer leurs œuvres, et pour cause…
Celui-ci, n’est né officiellement qu’en 1795 !

On sait, grâce à divers auteurs anciens, tels que Héron, que dès l’antiquité les premières mesures ont été prises des dimensions du corps humain, ce que confirment d’ailleurs les noms de : pas, coudée, pied, palme, pouce, doigt, encore employés de nos jours.

Au Moyen-âge, donc, les bâtisseurs utilisaient une pige constituées de cinq tiges articulées, correspondant chacune à une unité de mesure de l’époque : la paume, la palme, l’empan, le pied et la coudée.

    

A Chartres*1 cependant, comme à Reims et dans la plupart des autres cathédrales, ils utilisèrent un autre système… basé sur le nombre d’Or… !

I : Qu’est-ce que le nombre d’Or ?

Les Romains, les Grecs, les Juifs et les Egyptiens étaient tous d’accord : 1,618 était le nombre d’Or.

Le nombre de l’harmonie universelle, le nombre de la création, le nombre de Dieu le Créateur. Chez les Grecs, avec le développement de la géométrie, la secte secrète des pythagoriciens en avait fait un symbole d’harmonie universelle, de vie, d’amour et de beauté.

Au Moyen-âge, les savants, les pères de l’église, les bâtisseurs, les maîtres d’ouvrages ou maîtres d’oeuvre, se réclamant de la doctrine platonicienne des corps cosmiques, (les cinq polyèdres réguliers), ont fait du nombre d’or, "la divine proportion", un modèle de perfection esthétique et philosophique.

Le nombre d'Or est appelé Phi

On le désigne par la lettre grecque (phi) en hommage au sculpteur grec Phidias (né vers 490 et mort vers 430 avant J.C) qui l’utilisa entre autre pour le Parthénon à Athènes.

II : Le nombre d’Or et son histoire

- Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d’Or dans le Temple d’Andros (découvert sous la mer des Bahamas).

- 2800 av JC : La Pyramide de Kheops*2 a des dimensions qui mettent en évidence l’importance que son architecte attachait au nombre d’Or. D’après Hérodote, des prêtres égyptiens disaient que les dimensions de la Grande Pyramide avaient été choisies telles que : "Le carré construit sur la hauteur verticale égalait exactement la surface de chacune des faces triangulaires"

 

- Au Ve siècle avant J-C. (447-432 av J-C) : Le sculpteur grec Phidias utilise le nombre d’Or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d’Athéna Parthénos. Il utilise également la racine carrée de 5 comme rapport.

        

Parthénon et nombre d'Or

- Au IIIe siècle avant J-C. : Euclide évoque le partage d’un segment en "extrême et moyenne raison" dans le livre VI des Eléments et traite pour la première fois les propriétés géométriques du nombre φ.
- « Une droite est dite coupée en extrême et moyenne raison quand, comme elle est toute entière relativement au plus grand segment, ainsi est le plus grand relativement au plus petit ». (Euclide, Eléments, livre VI, 3ème définition).*3

Euclide

- 1175 : Fibonacci né à Pise, de son vrai nom Léonardo Pisano. (Fibonacci est un surnom qui vient de filius Bonacci qui veut dire fils de Bonacci).
Il était l’un des plus grands mathématiciens du Moyen-âge.

Fibonacci

C’est lui qui a introduit la numération décimale et l’écriture arabe des chiffres en Occident, en ramenant d’Algérie (où travaillait son père) dans son livre Liber abaci (1202), les connaissances acquises sur les méthodes algébriques et les problèmes. Dans cet ouvrage, il émet l'idée que l’arithmétique et la géométrie sont liés, mais aussi il met l’accent sur les neufs symboles indous de la numération !... ainsi que le signe zéro.

Rappelons que dans la célèbre suite de Fibonacci, chaque nombre est obtenu en ajoutant les deux nombres qui le précèdent :

0      1     1     2     3     5     8     13     21     34     55     89     144     233 ...

Fibonacci fut sans doute le mathématicien le plus habile de toute l’époque médiévale chrétienne.

- 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit "La divine proportion" illustrée par Leonard de Vinci...

Leonard de Vinci

- Au XIXème siècle : Adolf Zeising (1810-1876), docteur en philosophie et professeur à Leipzig puis Munich, parle de "Section d’Or" (der goldene Schnitt) et s’y intéresse non plus à propos de géométrie mais en ce qui concerne l’esthétique et l’architecture. Il cherche ce rapport, et le trouve dans beaucoup de monuments classiques.

C’est lui qui introduit le côté mythique et mystique du nombre d’Or.

- Au début du XXème siècle : Matila Ghyka, diplomate roumain, s’appuie sur les travaux du philosophe allemand Zeising et du physicien allemand Gustav Théodore Fechner, ses ouvrages : L’esthétique des proportions dans la nature et dans les arts (1927) et Le Nombre d’Or, Rites et rythmes pythagoriciens dans le développement de la civilisation occidentale (1931) insistent sur la prééminence du nombre d’Or et établissent définitivement le mythe .

- Au cours du XXème siècle : des peintres tels Dali et Picasso, ainsi que des architectes comme Le Corbusier, eurent recours au nombre d’Or.

La Cène par Dali

III : Pourquoi utiliser le nombre d’Or ?

Phi apparaît dans toute la vie et l’univers !
Il est une constante universelle de conception, la signature de Dieu.

Il est le nombre utilisé partout dans l’ordre caché de la Création et qu’il fallait donc employer dans les édifices dédiés au Créateur afin de s’en rapprocher. Empreint de mystère, objet d’un culte tantôt religieux, tantôt magique, le nombre d’Or va influencer la vision occidentale de l’harmonie.

Cette même proportion est utilisée pour réaliser l’équilibre, l’harmonie et la beauté dans les créations d’art, d’architecture, de couleurs, de conception, de composition, d’espace et même de musique.

Nous venons de voir que La suite de Fibonacci consiste à additionner les deux termes précédents (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ...) et le rapport entre chaque terme (2/1, 3/2, 5/3 ...) correspond au nombre d'or : 1,618 !

Or la proportion 2/1 est celle de la pyramide de Kheops, des Temples Egyptiens et Grecs mais aussi celle du Temple de Salomon… !

Le nombre d’Or véritable petit nirvana arithmétique, a été depuis des temps immémoriaux, une voie privilégiée de communication avec l’au-delà...

IV : Définition et valeur du Nombre d'Or

Le nombre d'or est la solution positive de l'équation :

C’est-à-dire le nombre

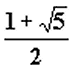
soit pour les cent premières décimales : 1,618 033 988 749 894 848 204 586 834 365 638 117 720 309 179 805 762 862 135 448 622 705 260 462 189 024 497 072 072 041

V : le nombre d’Or et la géométrie de la vie…

Phi apparaît entre autre dans :

Les proportions du corps humain

Les proportions de beaucoup d'animaux

La structure de l’ADN

Le système solaire

La Nature en général...

quelques exemples:

Le nautile et son développement combinent la suite de Fibonacci et le nombre d'Or...

           

Le tournesol et sa double spirale inversé, là aussi Fibonacci et le nombre d'Or !

VI : Conclusion

Les Templiers étaient certes des moines soldats, mais c’étaient aussi, et avant toute chose pour certains d'entres eux des Initiés.

Je ne saurais prétendre que tous eurent accès aux arcanes cachés de la Tradition Primordiale, appelée aussi Sagesse Immémoriale, (la Connaissance Occulte), car ce serait ignorer les lois qui régissent l’initiation humaine et solaire.

Mais on ne peut nier indéfiniment qu’ils réalisèrent la synthèse des hermétismes orientaux et occidentaux, et qu’ils en furent les valeureux et dignes dépositaires… 

Un Abraxas

* 1 Je reviendrai sur les liens unissant la Cathédrale de Chartre et la pyramide de Kheops …

* 2 La COUDEE ROYALE EGYPTIENNE dénommée mesure de l'Initié… est estimée au 19ème siècle à 52,36 cm.

Cette suite est aussi géométrique puisque le rapport entre deux mesures consécutives est le nombre d’Or. Nous le visualisons très bien sur la suite des pentagones du schéma ci-dessous.

* 3 Le partage en "extrême et moyenne raison" d’un segment :

Un segment est partagé suivant la section d’Or ou la proportion divine si les rapport x / y et y / (x - y) sont égaux, ce qui signifie que le petit et le moyen segment sont dans le même rapport que le moyen et le grand segment.

De l’équation :  ,  on obtient l'équation 

dont le résultat est : =

Comments

[Le veilleur]

Il n'y a pas de but ?

Où ne le percevez-vous pas...



La source est ailleurs, oui en effet.



Oubliez votre mental... je vous retourne ce conseil que je fais mien depuis fort longtemps...

Amicalement

Le Veilleur

[ET]

Le ménage est fait. Chaque matin.....

Je n'ai pas de question....ni d'affirmation...

Mon mot n'est qu'un propos....la syntaxe importe peu la ponctuation encore moins..tout çela n'est pas la Verité.....

La quête du Grall...le prieuré de Sion...l'intelligence veille...il n'y a pas de but...simplement du sens....oubliez votre mental...la source est ailleurs.....

[Le veilleur]

Votre commentaire semble être une question :

et si tout cela n'était qu'élucubrations ?

Pourtant, en guise de ponctuation, au lieu du traditionnel point d'interrogation, vous nous gratifiez de 4 points d'exclamations...

Il est donc impossible de savoir si vous questionnez, ou si vous affirmez...

Devant une telle confusion il est difficile de vous apporter le moindre éclaircissement...

Le plus simple serait de faire le ménage en vous.

Fraternellement

Le Veilleur

[ET]

et si tout cela n'était qu'élucubrations !!!!

[tibbe]

Merci pour votre article, ce qui m'a induit en erreur c'est que j'ai cru, dans votre texte, que vous disiez que le rapport des nombres n/n-1 donnait le nombre d'or mais en fait il est proche soit supérieur soit inférieur et plus on va monter dans la suite plus il va s'en approcher. Bon, ok, ce que je ne comprends pas, à présent, c'est le sens de tout ca / rapport à sa suite, et l'intérêt que cela présente puisque visiblement les intérêts sont immenses.

frat